Teooria: Ruutvõrrand

Ruutvõrrand on kujul:

\[ ax^2 + bx + c = 0 \]

kus \(a\), \(b\), ja \(c\) on arvud ning \(a \neq 0\). See tähendab, et tundmatu on ruudus ning võrrandi graafikuks on parabool.

---

Lahendvalem

Ruutvõrrandi lahendvalem on:

\[ x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

Selle valemiga saad leida ruutvõrrandi lahendid, ehk kohad kus graafik puudutab x-telge. Siinkohal on oluline meeles pidada, et kõikide ruutvõrrandite graafikud ei puuduta x-telge ja seetõttu pole neil ka reaallahendeid . Et teada, kas ruutvõrrandil on lahendid, võtame appi diskriminandi.

---

Diskriminant

Lahendite arvu määramiseks kasutame diskriminanti, selle leiame me lahendvalemist, ja see on osa mis jääb ruutjure alla:

\[ x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-b \pm \sqrt{D}}{2a} \] \[ D = b^2 - 4ac \]

Diskriminant näitab, mitu pärislahendit ruutvõrrandil on.

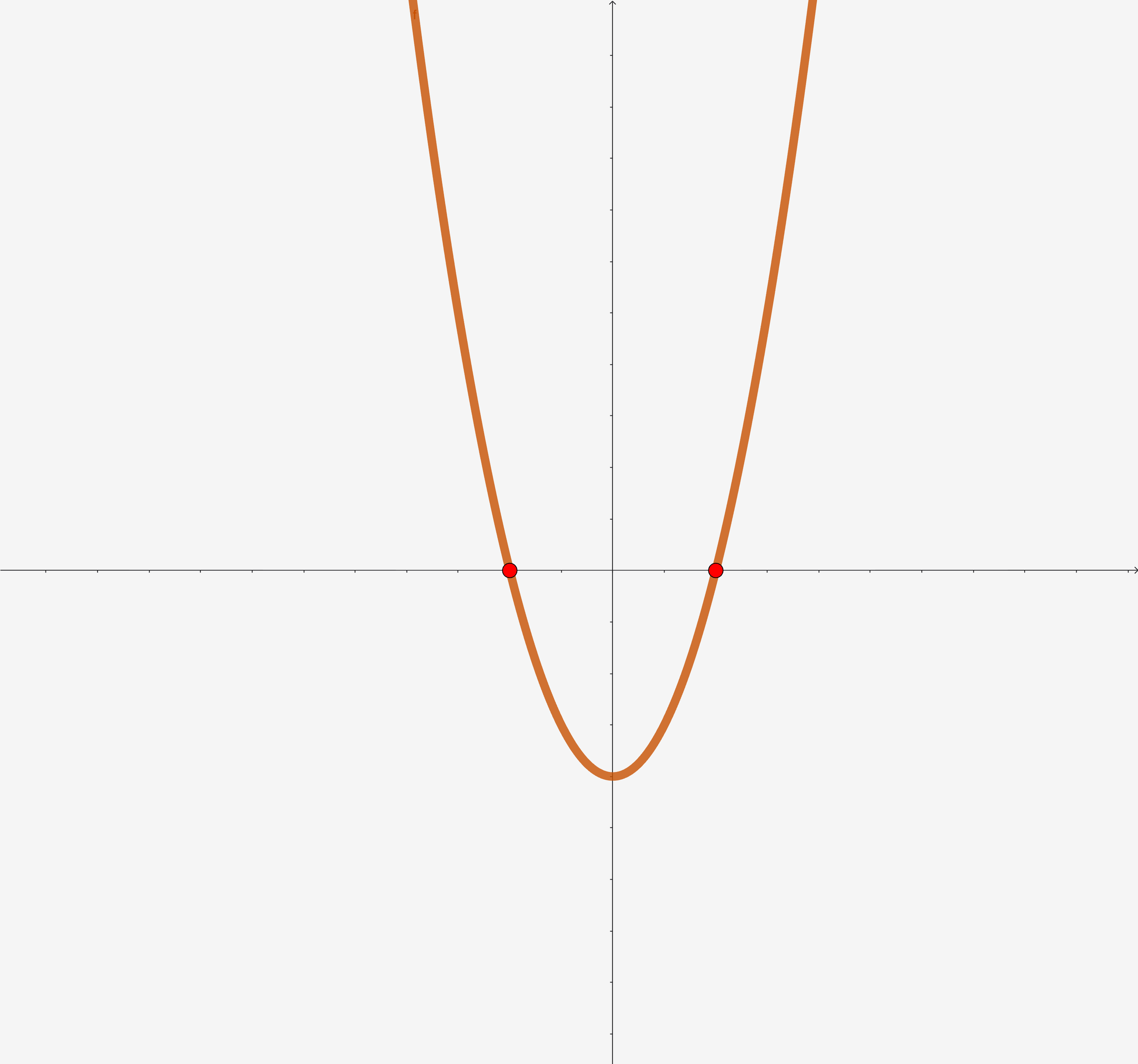
• Kui \(D > 0\) – kaks erinevat lahendit (parabool lõikab x-telge kahes punktis)

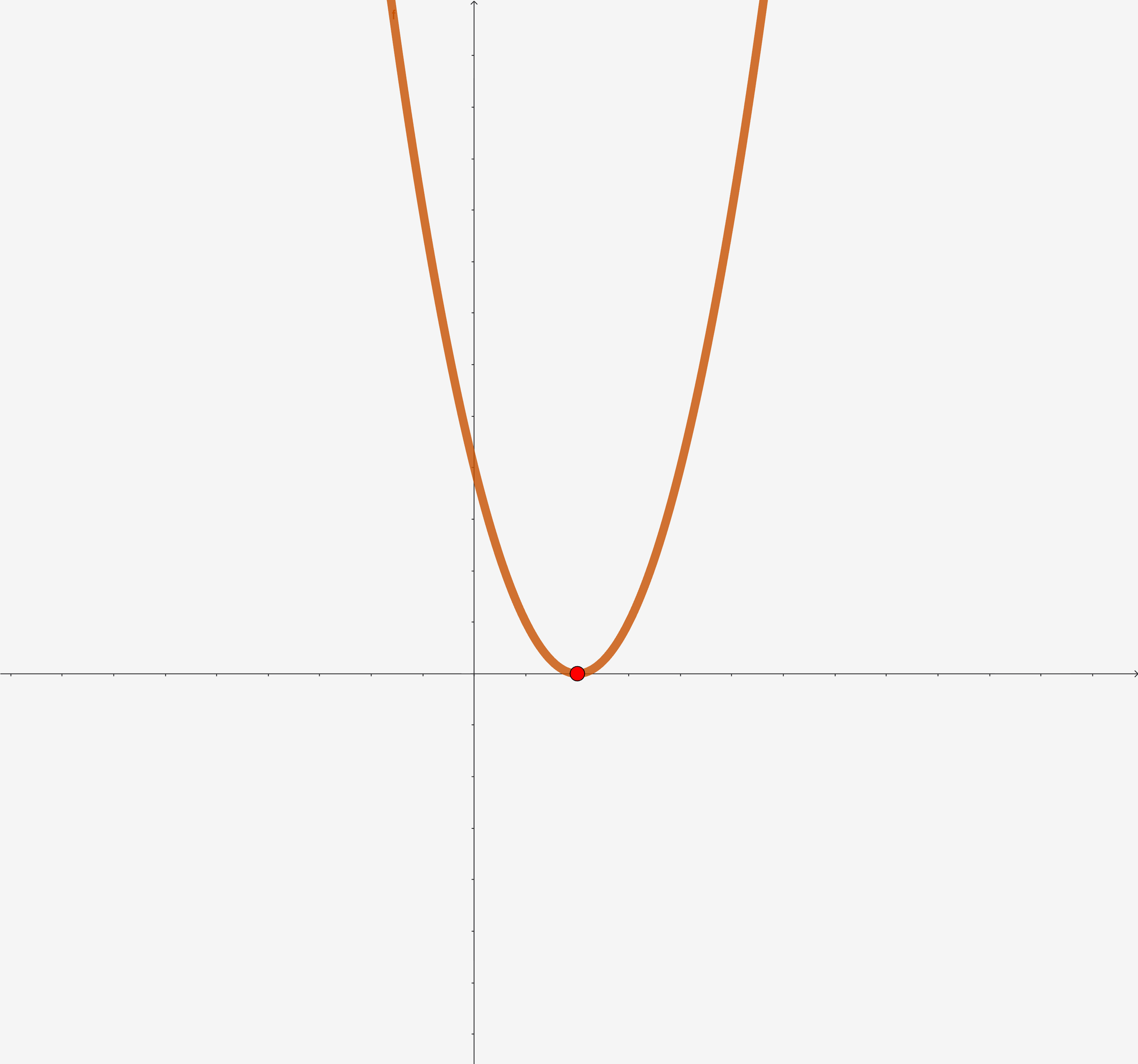
• Kui \(D = 0\) – kaks võrdset lahendit (parabool puudutab x-telge)

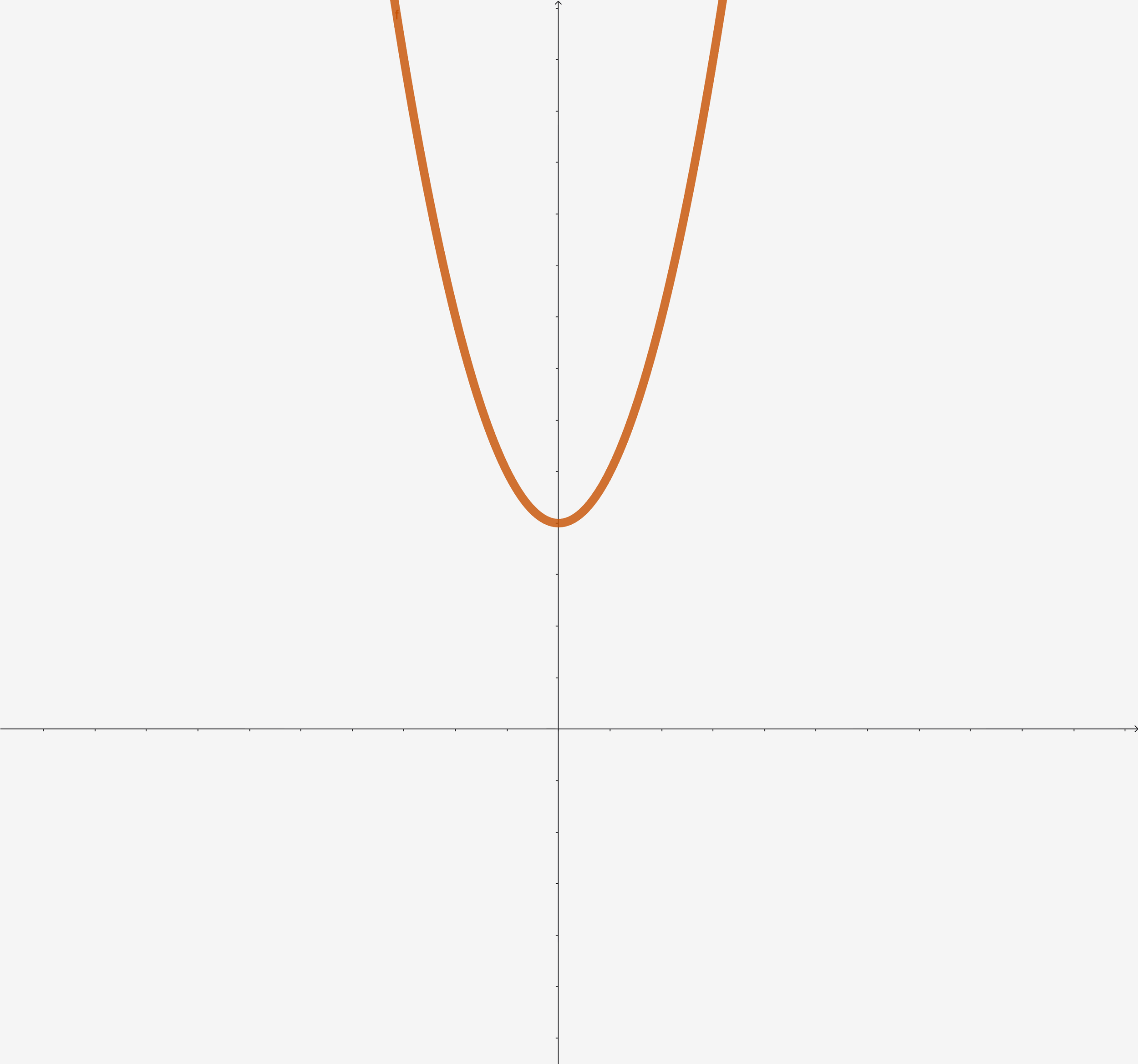
• Kui \(D < 0\) – pärislahendeid ei ole (parabool ei lõika x-telge)

---

Näide 1

Lahendame võrrandi:

\[ 2x^2 + 3x - 2 = 0 \]

Siin \(a = 2\), \(b = 3\), \(c = -2\).

Arvutame diskriminandi:

\[ D = 3^2 - 4 \cdot 2 \cdot (-2) = 25 \]

Kuna \(D > 0\), on kaks erinevat lahendit.

Arvutame lahendid:

\[ x_{1,2} = \frac{-3 \pm \sqrt{25}}{4} \] \[ x_1 = \frac{-3 + 5}{4} = \frac{2}{4} = 0.5 \] \[ x_2 = \frac{-3 - 5}{4} = \frac{-8}{4} = -2 \]

Näide 2

Lahendame võrrandi:

\[ x^2 - 4x + 4 = 0 \]

Siin \(a = 1\), \(b = -4\), \(c = 4\).

Arvutame diskriminandi:

\[ D = (-4)^2 - 4 \cdot 1 \cdot 4 = 16 - 16 = 0 \]

Kuna \(D = 0\), on kaks võrdset lahendit (topeltjuur).

Arvutame lahendi:

\[ x_{1,2} = \frac{-b}{2a} = \frac{-(-4)}{2 \cdot 1} = \frac{4}{2} = 2 \]

Seega on võrrandi lahend:

\[ x_{1,2} = 2 \]

---

Taandatud ruutvõrrand

Kui ruutvõrrandit saab kirjutada kujul

\[ x^2 + px + q = 0, \]

siis nimetatakse seda taandatud ruutvõrrandiks. See on ruutvõrrandi erivorm, kus ruutliikme kordaja on 1 (ehk \(a = 1\)). Sellisel juhul kaob kordaja \(a\) lahendvalemist ja valem muutub oluliselt lihtsamaks.

Taandatud ruutvõrrand on oluline, sest sellega seostub lihtsam versioon Viete teoreemist:

\[ x_1 + x_2 = -p, \qquad x_1 \cdot x_2 = q. \]

See teeb lahendite summa ja korrutise leidmise eriti kiireks ning muudab mõnede ruutvõrrandite lahendamise võimalikuks lausa peast.

Näide 3: Ruutvõrrandi lahendamine kiiresti Viete abil

Vaatame ruutvõrrandit:

\[ x^2 - 5x + 6 = 0 \]

See on taandatud ruutvõrrand kujul \(x^2 + px + q = 0\), kus \(p = -5\) ja \(q = 6\).

Viete teoreemi järgi kehtib:

\[ x_1 + x_2 = -p = 5, \qquad x_1 \cdot x_2 = q = 6. \]

Seega peame leidma kaks arvu, mille:

• summa on 5,
• korrutis on 6.

Sellised arvud on 2 ja 3, sest:

\[ 2 + 3 = 5, \qquad 2 \cdot 3 = 6. \]

Seega lahendid on:

\[ x_1 = 2, \qquad x_2 = 3. \]

Saime vastuse ilma lahendvalemit kasutamata – lihtsalt otsides kaks sobivat arvu. Selline Viete abil lahendamine on kiire ja mugav, eriti taandatud ruutvõrrandite puhul. NB! Kui sa ei ole sellise trikiga mugav, kasuta alati lahendvalemit. See kehtib alati ja vähendab tõenäosust, et teed lahendades vea.